Broadly speaking, two classes of theories of semantic memory have been put
forth to account for semantic priming in lexical tasks. Spreading-activation
theories (e.g., Anderson, 1983; Collins & Loftus, 1975; McNamara, 1992a, 1992b, 1994) propose that semantic memory consists of a network
of interconnected nodes, each representing a particular concept. Processing a
word involves activating the concept node in semantic memory corresponding to
its meaning. This activation is assumed to spread along links to other,
related concepts, thereby facilitating the subsequent processing of those
concepts. By contrast, compound-cue theories (e.g., Dosher & Rosedale, 1989; McKoon & Ratcliff, 1992; Ratcliff & McKoon, 1988, 1994) propose that, in processing a word, semantic
memory is accessed using a cue consisting of the word conjoined with the
context in which it occurs (e.g., the preceding word). Semantically related
words co-occur more frequently than do unrelated words, and so the compound
cues for related words tend to have greater familiarity than do those for
unrelated words. In many general models of memory retrieval (e.g., Gillund & Shiffrin, 1984; Hintzman, 1986; Murdock, 1982),
greater familiarity gives rise to faster and more accurate processing,
resulting in semantic priming.
Recently, a third type of theory has been proposed to account for semantic
priming, based on distributed connectionist networks (Kawamoto, 1988; Masson, 1991, 1995; McRae, de Sa, &
Seidenberg, 1993; Sharkey & Sharkey,
1992). In such networks, each concept is represented, not by a particular
unit, but by a particular pattern of activity over a large number of
processing units. Related concepts are represented by similar (i.e.,
overlapping) patterns of activity. Each unit can be thought of as encoding a
particular semantic feature that participates in many concepts (Smith & Medin, 1981), although these features need
not correspond to verbalizeable attributes of any concept. In processing a
word, units cooperate and compete across weighted connections until the network
as a whole settles into a stable pattern of activity that represents the
meaning of the word. If the network starts from this pattern in processing a
subsequent word, it will be faster to settle for a related than for an
unrelated word because many of the units will already be in their correct
states.
Distributed network theories bear an interesting relationship both to
spreading-activation theories and to compound-cue theories. Although, in some
sense, activation ``spreads'' among units in a distributed network, this spread
is not between concepts but between features. For a given pattern of activity,
the degree to which any concept is ``active'' depends on its overlap with the
current pattern. After settling into the meaning of a word, related meanings
are active simultaneously (to the degree that they are similar)---no
additional spread of activation is required. Thus, distributed network
theories provide a more natural interpretation of the finding that, while the
degree of relatedness influences the magnitude of priming, it does not
influence its time of onset, which is essentially instantaneous (Lorch, 1982; Ratcliff & McKoon, 1981). In some ways,
distributed network theories are more similar to compound-cue theories, in that
the processing of a word is sensitive to the context in which it occurs (as
reflected in the current state of the network). However, conjunctions need not
be represented explicitly, so that processing can depend on properties of
contexts independent of their co-occurrences with target words. Thus, for
instance, distributed network theories can account naturally for the finding
that different neutral contexts (e.g., unrelated words, neutral words like
READY, and nonwords) have equivalent effects on between-trial priming, even
though their familiarities as compounds with target words are very different
(McNamara, 1994).
Unfortunately, two sets of empirical findings appear to pose problems for
distributed network theories of semantic priming. The first relates to
findings that different types of relations among words influence priming in
different ways. In particular, one can distinguish an associative
relation among words (e.g., as measured by free association norms; Postman & Keppel, 1970) from a purely semantic
relation (i.e., having similar meanings, such as category co-ordinates).
Associatively related word pairs are typically also semantically related (e.g.,
BREAD-BUTTER) but many semantically related word pairs are not associatively
related (e.g., BREAD-CAKE). In the few studies that have studied priming among
words that are semantically but not associatively related (e.g., Fischler, 1977; Seidenberg, Waters, Sanders, & Langer,
1984), the priming effect is much smaller than that found for associatively
related words, particularly in lexical decision, and the effect was completely
absent under conditions which prevent expectancies and post-lexical checking
(Shelton & Martin, 1992). Furthermore,
unlike semantic priming, associative priming is highly asymmetric; for example,
BED-PAN produces strong priming whereas PAN-BED produces little if any
(particularly in naming; see Neely, 1991).
Similar dissociations between semantic and associative effects have been
demonstrated using cross-model priming in sentence contexts (Moss & Marslen-Wilson, 1993) and in
the degeneration of semantic memory in Alzheimer's disease (Glosser & Friedman, 1991). These data
are problematic for distributed network theories (e.g., Kawamoto, 1988; Masson, 1995) because they typically employ only a
single, symmetric manipulation---pattern overlap---to encode word relatedness.
There is no opportunity for different types of relations among words---semantic
and associative---to behave differently.
The second set of findings that has challenged distributed network theories
is that associative priming can span an intervening unrelated item, such as in
the word sequence BREAD-DOG-BUTTER, although it is very weak under these
conditions (Joordens & Besner, 1992; McNamara, 1994). In a distributed network, if the entire
network settles completely to the meaning of the intervening word DOG, then the
pattern of activity representing the meaning of BREAD will be completely
eliminated, leaving no opportunity for it to facilitate the processing of
BUTTER. Masson (1995) considered the possibility that the intervening word
might be processed only partially, leaving residual semantic activation from
BREAD to influence
BUTTER. Using a Hopfield (1982) network, he
simulated the small priming effect across unrelated words in a naming task by
basing the network's response on the activity of phonological units which were
updated more frequently than semantic units. Unfortunately, the simulations
used a very small vocabulary (only three pairs of semantically related items),
and no independent justification was provided for why phonological and semantic
units should behave differently.
The current paper presents a distributed network model of priming that
addresses the challenges posed by associative vs. semantic priming and by
priming across an unrelated item. The model differs from previous ones in two
main ways. First, whereas semantic relatedness among words is encoded by the
degree of overlap of their semantic feature representations, an association
from one word to another is encoded directly in the likelihood that the one
follows the other during training (see Moss, Hare, Day,
& Tyler, 1994 for a similar approach). Second, a more powerful learning
procedure is used---continuous back-propagation through time (Pearlmutter, 1989). This procedure has the critical
properties that unit states change gradually over time in response to input,
and that learning is sensitive to the entire trajectory from the initial
activity pattern to the final activity pattern. The model also replicates a
number of basic findings in the priming literature, including greater priming
for low-frequency targets, degraded targets, and high-dominance category
exemplars.
The semantic representations of words were generated artificially but with
considerable structure. Eight different random patterns were generated over
100 semantic features, in which each unit had a probability of 0.1 of being
active. These patterns served as the ``prototypes'' for eight separate
semantic categories. Sixteen category exemplars were generated from each
prototype pattern by randomly altering some of its features (Chauvin, 1988). Eight of these were typical or
high-dominance exemplars in which relatively few features of the prototype were
changed (each feature had a probability of 0.2 of being resampled with a
probability of 0.1 of being active). The remaining eight were atypical or
low-dominance exemplars in which many more features were altered (resampling
probability of 0.4). The effect of this manipulation is simply to make all
exemplars in a category cluster around the prototype, with high-dominance
exemplars more similar to the category prototype than low-dominance exemplars.
Words will be considered semantically related if they were generated from the
same prototype.
The resulting 128 semantic representations were randomly assigned
orthographic representations consisting of patterns of activity over 20
orthographic units. These patterns were generated randomly such that each unit
had a probability of 0.1 of being active, with the constraint that every
pattern had at least two active units, and all pairs of patterns differed in
the activities of at least two units. No attempt was made to model
orthographic relatedness among words; the orthographic patterns simply
guaranteed that the written forms of words were fairly sparse and were
discriminable from each other. For the current purposes, the critical property
of this artificial task is that, although there are systematic relationships
among word meanings, there is no systematic relationship between the written
form of a word and its meaning.
Within each dominance class of each category, half of the words were
designated as high-frequency and the other half as low-frequency. Each word
was also assigned a single associated word, under the constraints that 1) every
word was the associate of some other word; 2) associated words were never
semantically related (i.e., in the same category); and 3) there were no mutual
associations among word pairs (i.e., no two words were each other's associate).
The frequency of a word and its association influenced how it was selected for
presentation during training, as described below.
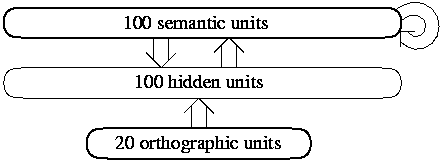
Figure 1:
The architecture of the network. Arrows represent full connectivity
between or within groups of units.
The states of units in the network change smoothly over time in response to
influences from other units. For the purposes of simulation on a digital
computer, it is convenient to approximate continuous units with finite
difference equations, in which time is discretized into ticks of some
duration 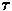 . Thus,
the input to unit j at time t is given by
. Thus,
the input to unit j at time t is given by
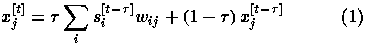
where 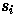 is the state of unit i
and
is the state of unit i
and 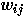 is the weight from unit i
to unit j. According to this equation, a unit's input at each time
tick is a weighted average of its current input and that dictated by other
units, where
is the weight from unit i
to unit j. According to this equation, a unit's input at each time
tick is a weighted average of its current input and that dictated by other
units, where 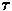 is the weighting
proportion. A relatively large value of
is the weighting
proportion. A relatively large value of 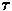 is used during most of training (0.2 in the current simulation),
when minimizing computation time is critical, whereas a much smaller
is used during most of training (0.2 in the current simulation),
when minimizing computation time is critical, whereas a much smaller 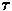 is used during testing (e.g., 0.01), when a
more accurate approximation of the underlying continuous system is desired.
is used during testing (e.g., 0.01), when a
more accurate approximation of the underlying continuous system is desired.
The state 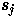 of unit j at
time t is simply the standard logistic or sigmoid function of its
current input,
of unit j at
time t is simply the standard logistic or sigmoid function of its
current input,
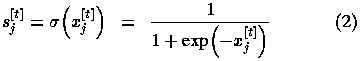
where exp(.) is the exponential function.
Training Procedure. The network was trained in the
following way. A word was presented to the network by clamping the states of
the orthographic units to its assigned representation, distorted by a slight
amount of random gaussian noise (with mean 0.0 and SD 0.05). On most
trials, all other units retained the inputs and states they had at the end of
processing the previous word. However, for the very first word, and with a
probability of 0.01 throughout training, these units were given reinitialized
inputs of 0.0 and states of 0.2. Then, for every time tick t of
duration 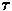 =0.2 over a total of 4.0 units
of time, units in the network updated their states according to Equations 1 and
2. (Note that the absolute time scale of the network is arbitrary.) A
continuous version of back-propagation through time (Pearlmutter, 1989) was used to calculate changes to the
connection weights that would reduce the discrepancy (measured using
cross-entropy; see Hinton, 1989) between
activations of the semantic units over the last 2.0 units of time and their
correct activations for the presented word. This temporally extended error
signal pressures the network to settle to the correct pattern as quickly as
possible. After each word presentation, the weights were updated immediately
(with a learning rate
=0.2 over a total of 4.0 units
of time, units in the network updated their states according to Equations 1 and
2. (Note that the absolute time scale of the network is arbitrary.) A
continuous version of back-propagation through time (Pearlmutter, 1989) was used to calculate changes to the
connection weights that would reduce the discrepancy (measured using
cross-entropy; see Hinton, 1989) between
activations of the semantic units over the last 2.0 units of time and their
correct activations for the presented word. This temporally extended error
signal pressures the network to settle to the correct pattern as quickly as
possible. After each word presentation, the weights were updated immediately
(with a learning rate 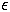 =0.005 and
momentum
=0.005 and
momentum 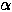 =0.8) and the next word was
chosen and presented. With a probability of 0.2, the next word chosen was the
associate of the previous word. On the remaining trials, the probability that
words were selected for training depended on their assigned frequency, such
that high-frequency words were twice as likely to be trained as low-frequency
words.
=0.8) and the next word was
chosen and presented. With a probability of 0.2, the next word chosen was the
associate of the previous word. On the remaining trials, the probability that
words were selected for training depended on their assigned frequency, such
that high-frequency words were twice as likely to be trained as low-frequency
words.
After 50,000 word presentations, 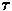 was reduced from 0.2 to 0.05, and after 3000 more presentations it was reduced
to 0.01 for a final 2000 presentations. At this point, the network was
completely accurate in settling into the semantic representation of each word,
regardless of the preceding context.
was reduced from 0.2 to 0.05, and after 3000 more presentations it was reduced
to 0.01 for a final 2000 presentations. At this point, the network was
completely accurate in settling into the semantic representation of each word,
regardless of the preceding context.
Testing Procedure. The reaction time (RT) of the trained
network in processing a word was defined as the time it took the network to
settle to the point where no semantic unit changed it state by more than an
output change tolerance of 0.001. Priming in the network occurs
because this settling time is influenced by the nature of the preceding prime
word(s) processed by the network. Typically, when testing the network, words
are presented in prime-target pairs. First, the network is initialized to
inputs of 0.0 and states of 0.2. Then the prime word is presented (with no
noise) and processed for some variable duration (the stimulus onset asynchrony,
or SOA). At this point, the target replaces the prime and the settling time of
the network in response to the target is measured.
Primes can either be semantically related, associatively related, or
unrelated to the target. To obtain the most reliable estimates of RT means for
these various conditions, the RT for each word as target is measured when
preceded by every other word as prime. For each item, its RT when preceded by
each of the 15 other words in its category is averaged to yield a semantically
related RT mean. Similarly, its RTs when preceded by the 111 words that are
neither semantically nor associatively related yields an unrelated RT mean.
Finally, the item's RT when preceded by the single word for which it is the
associate is used as the associatively related RT value. These RT means were
calculated at SOAs of 0.25, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, and 4.0. The
manipulation of SOA is intended primarily to illustrate effects in
network---direct comparisons with empirical results are problematic because
longer SOAs are thought to introduce contaminating effects from
subject-generated expectancies and post-lexical checking (Balota & Chumbley, 1984; Seidenberg et al., 1984).
Results and Discussion
As in other distributed network models (e.g.,
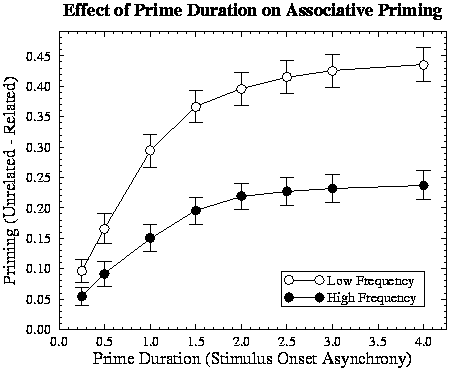
Figure 2:
Effect of the duration of the prime on associative priming for low-
and high-frequency targets.
Associative priming occurs in the network because, during training, it was
pressured to learn to make a rapid transition from the meaning of the prime to
the meaning of its associated word much more frequently than transitions to the
meanings of other words. High-frequency targets benefit less from this extra
support because semantic units are already being driven more strongly than for
low-frequency words; due to the asymptotic behavior of the logistic activation
function, any additional input to a unit yields diminishing changes in its
activation as it approaches the extremes of 0.0 or 1.0.
An equivalent analysis with the associated primes and targets reversed
revealed no significant backward associative priming nor any interactions (F<1
for all comparisons).
Semantic Priming.
A similar analysis was performed on the differences in RTs for unrelated primes
versus semantically related primes (e.g., BREAD-CAKE). The pattern of results
is quite different from that for associative priming. Semantic priming is much
weaker (mean 0.044; F[1,24]=29.96, p< .001), and it interacts with target
category dominance (means: high 0.062, low 0.027; F[1,124]=4.67, p=.033) rather
than frequency (F<1). Furthermore, the change in semantic priming over SOA
(F[7,868]=22.82, p< .001) is very different than for associative priming (see Figure 3 and compare with Figure 2 noting
the scale difference). In particular, semantic priming peaks at very short
SOAs then gradually declines as the prime is processed more fully. At
intermediate SOA values, such priming may even be too weak to detect
experimentally (as in the Shelton & Martin,
1992, study).
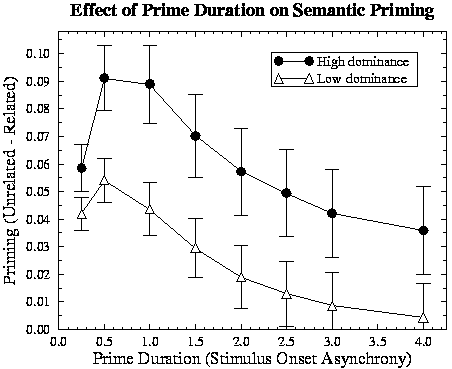
Figure 3:
Effect of the duration of the prime on semantic priming
for high- and low-dominance targets.
Why does semantic priming behave so differently compared with associative
priming? Early on in processing a semantically related prime, units move
towards a pattern that is similar to the pattern for the target, and this
benefits subsequent processing of the target as long as units are still within
the linear range of the logistic activation function. However, with additional
processing, units are driven to more extreme values, including those that
differ between the prime and target patterns. In order to identify
the target accurately, all of these differences must be corrected.
The time it takes for processing of the target to accomplish this is influenced
by the number of units the prime and target have in common (as indicated by the
effect of category dominance, matching the empirical findings), but this
influence is relatively weak. As the prime is processed more fully, the time
it takes to change the states of incorrect units is relatively independent of
the number of other, correct units, so that semantically related primes provide
almost no advantage over unrelated primes.
Target Degradation.
Empirical studies have found that priming is increased if targets are degraded
visually (e.g., by reducing contrast; see Neely,
1991). To investigate this effect in the model, the orthographic input
patterns for targets were reduced in visual contrast by scaling the input
values towards the neutral value of 0.2 by varying amounts (0.05, 0.10, 0.15,
and 0.2). For example, for a normal input of 1.0 and a degradation of 0.05,
the presented input value would be 1.0-0.05(1.0-0.2)=0.96. Reaction times to
degraded targets were measured when preceded by each word as a prime with an
SOA of 2.0. The differences between RTs for targets preceded by their
associatively related prime and their mean RTs when preceded by unrelated
primes were entered into an 2x4 ANOVA over items, with target frequency as a
between-item factor and target degradation as a within-item factor. Priming
was influenced reliably by word frequency (means: low 0.242, high 0.489;
F[1,126]=20.41, p< .001), replicating the effect found with non-degraded
targets. More importantly, there was greater priming for more highly degraded
targets (F[3,378]=6.683, p< .001; see
Figure 4). The interaction of frequency
and degradation was not reliable (F[3,378]=1.519, p=.209). Thus, the network
replicates the empirical finding that target degradation increases associative
priming.
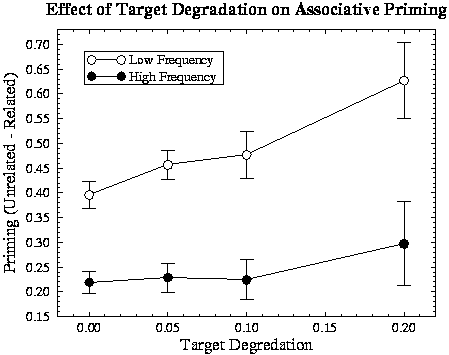
Figure 4:
Effect of the degree of degradation of the target on associative
priming for low- and high-frequency targets.
Priming Across Intervening Unrelated Items.
The final experiment tested the conditions under which associative priming
spanned an intervening unrelated item (e.g.,
BREAD-DOG-BUTTER). Such priming is observed empirically when items are
processed relatively briefly. For example, Joordens and Besner's (1992) subjects named each
stimulus item under a very short (300 msec) inter-trial interval, producing
naming latencies about 150 msec faster than in typical naming studies. These
testing conditions can be approximated with the model by having it process the
prime, the intervening item, and the target using a less-stringent criterion
for the degree to which the output must settle before the network responds.
Accordingly, the magnitude of associative priming across an unrelated item was
investigated across increasing values of the output change tolerance: 0.001
(the original value), 0.0015, 0.002, 0.003, and 0.004. To get a good estimate
of the associatively related RT means, each association was tested with every
other word in the corpus that was unrelated associatively and semantically to
both the prime and target as the intermediate item. The RT means for unrelated
primes were based on presenting every unrelated word as prime five times, each
with a different randomly selected unrelated word as the intervening item.
Responses in which the state of any semantic unit was not on the correct side
of 0.5 (no more than 1.3% of trials in any condition) were considered errors
and were excluded from the calculation of the means. The differences in RT
means between related and unrelated prime-target pairs were then subject to a
2x5 ANOVA over items, with target frequency as a between-item factor and output
change tolerance as a within-item factor. Figure 5 shows
the degree of priming across an unrelated item for high- and low-frequency
targets. There is a small but reliable overall priming effect (mean 0.012,
F[1,124]=33.5, p< .001) which is influenced both by frequency (F[1,124]=7.91,
p=.006) and by output change tolerance (F[4,496]=7.77, p< .001), and these
factors interact (F[4,496]=2.61, p=.035). Thus, the network exhibits
significant associative priming across an intervening unrelated item,
particularly under conditions which encourage fast responding (as found by Joordens & Besner, 1992).
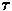 . Thus,
the input to unit j at time t is given by
. Thus,
the input to unit j at time t is given by 
 is the state of unit i
and
is the state of unit i
and 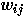 is the weight from unit i
to unit j. According to this equation, a unit's input at each time
tick is a weighted average of its current input and that dictated by other
units, where
is the weight from unit i
to unit j. According to this equation, a unit's input at each time
tick is a weighted average of its current input and that dictated by other
units, where 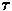 is the weighting
proportion. A relatively large value of
is the weighting
proportion. A relatively large value of 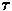 is used during most of training (0.2 in the current simulation),
when minimizing computation time is critical, whereas a much smaller
is used during most of training (0.2 in the current simulation),
when minimizing computation time is critical, whereas a much smaller 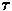 is used during testing (e.g., 0.01), when a
more accurate approximation of the underlying continuous system is desired.
is used during testing (e.g., 0.01), when a
more accurate approximation of the underlying continuous system is desired.

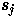 of unit j at
time t is simply the standard logistic or sigmoid function of its
current input,
of unit j at
time t is simply the standard logistic or sigmoid function of its
current input,
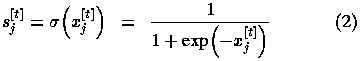
 =0.005 and
momentum
=0.005 and
momentum  =0.8) and the next word was
chosen and presented. With a probability of 0.2, the next word chosen was the
associate of the previous word. On the remaining trials, the probability that
words were selected for training depended on their assigned frequency, such
that high-frequency words were twice as likely to be trained as low-frequency
words.
=0.8) and the next word was
chosen and presented. With a probability of 0.2, the next word chosen was the
associate of the previous word. On the remaining trials, the probability that
words were selected for training depended on their assigned frequency, such
that high-frequency words were twice as likely to be trained as low-frequency
words.



